实验目的
1.用电测法测定同种材料自由叠合梁横截面上的应变、应力分布规律。
2.由实验结果得出叠梁横截面上的正应力分布规律并与单体梁进行比较。
3.通过实验和理论分析深化对弯曲变形理论的理解,建立力学计算模型的思维方法。
二、实验设备
1.YE2539程控应变仪。
2.力学多功能实验台。
3.贴有电阻应变片的矩形截面组合梁(钢-钢组合梁)。
钢-钢组合梁的上半部为Q235钢,弹性模量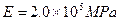 ,下半部为45号钢,弹性模量
,下半部为45号钢,弹性模量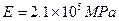
三、实验原理
由材料力学纯弯曲理论可知单根矩形截面梁的应力分布沿截面高度按线性规律分布,横截面在中性轴位置处的应力为零,距离中性轴的上、下边缘处的正应力最大。
但在实际工程结构中,经常遇到由两根以上的梁共同组合而成的组合梁。例如汽车缓冲板簧、吊车轨道梁是钢筋混凝土梁与钢轨共同承担吊车的重量。本次实验对象为两根同截面尺寸、同材料的钢梁,采用钢-钢自由叠合梁,叠合梁实验装置及横截面上各点应变片的位置如下图。
所谓叠梁,是两根矩形截面梁上下叠放在一起,两界面间加润滑剂,如图1所示。两根梁的材料可相同,也可不同;两根梁的截面高度尺寸可相同,亦可相异。只要保证在变形时两梁界面不分离即可。
图1所示的叠梁,在弯矩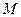 的作用下,可以认为两梁界面处的挠度相等,并且挠度远小于梁的跨度;上下梁各自的中性轴,在小变形的前提下,各中性层的曲率近似相等。从而,可以应用平衡方程和弯曲变形的基本方程等建立弯矩
的作用下,可以认为两梁界面处的挠度相等,并且挠度远小于梁的跨度;上下梁各自的中性轴,在小变形的前提下,各中性层的曲率近似相等。从而,可以应用平衡方程和弯曲变形的基本方程等建立弯矩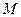 、
、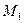 和
和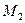 之间的关系如下:
之间的关系如下:
叠梁横截面弯矩
 (1)
(1)
中性层的曲率为
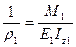 ;
;  ;
; 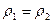 (2)
(2)
由以上两式得上、下梁的弯矩分别为
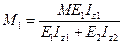 (3)
(3)
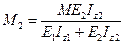 (4)
(4)
式中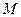 为总弯矩;
为总弯矩;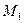 和
和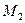 分别为上下梁各自承担的弯矩;
分别为上下梁各自承担的弯矩;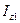 为叠梁1截面对
为叠梁1截面对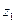 轴的惯性距;
轴的惯性距;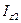 为叠梁2截面对
为叠梁2截面对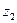 轴的惯性距;
轴的惯性距; 和
和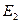 分别为上下梁的弹性模量,
分别为上下梁的弹性模量, 和
和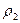 为上下梁的曲率半径。
为上下梁的曲率半径。
因此,可得到叠梁Ⅰ和叠梁Ⅱ正应力理论计算公式分别为
 (5)
(5)
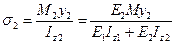 (6)
(6)
式中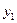 ——叠梁Ⅰ上测点距
——叠梁Ⅰ上测点距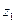 轴的距离;
轴的距离;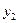 ——叠梁Ⅱ上测点距
——叠梁Ⅱ上测点距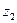 轴的距离。
轴的距离。
实验时,在梁纯弯曲段沿横截面高度自上而下选8个测点,在测点表面沿梁轴方向各粘贴一枚电阻应变片,当对梁施加弯矩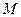 时,粘贴在各测点的电阻应变片的阻值将发生变化。从而根据电测法的基本原理,就可测得各测点的线应变值。
时,粘贴在各测点的电阻应变片的阻值将发生变化。从而根据电测法的基本原理,就可测得各测点的线应变值。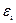 (角标
(角标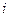 为测点号,
为测点号,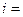 1,2,3,…,8)。
1,2,3,…,8)。
由于各点处于单向应力状态,由虎克定律求得各测点实测应力值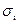 ,即
,即
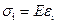 (7)
(7)
按式(5)、(6)分别计算出上、下梁的各点应力值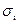 。
。
然后将实验值与理论值进行比较,通过该实验,以明确叠梁横截面上的应力分布规律。
四、实验步骤
1.叠梁的单梁截面宽度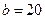 mm,高度
mm,高度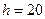 mm,荷载作用点到梁支点距离
mm,荷载作用点到梁支点距离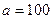 mm。
mm。
2.将荷载传感器与测力仪连接, 接通测力仪电源, 将测力仪开关置开。
3.将梁上应变片按半桥单臂工作接至应变仪通道上。
4.本实验取初始荷载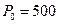 N,
N,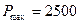 N,
N,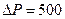 N共分五级加载。
N共分五级加载。
5.加初始荷载 N,将各通道初始应变均置零。
N,将各通道初始应变均置零。
6.逐级加载,记录各级荷载作用下各点的应变读数。